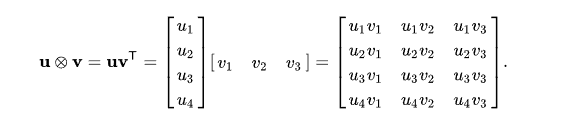Beating OpenBLAS in FP32 Matrix Multiplication
This is an updated version of Beating NumPy’s Matrix Multiplication in 150 Lines of C Code. The revised blog post includes improved performance, detailed benchmarking information, and minor text updates.
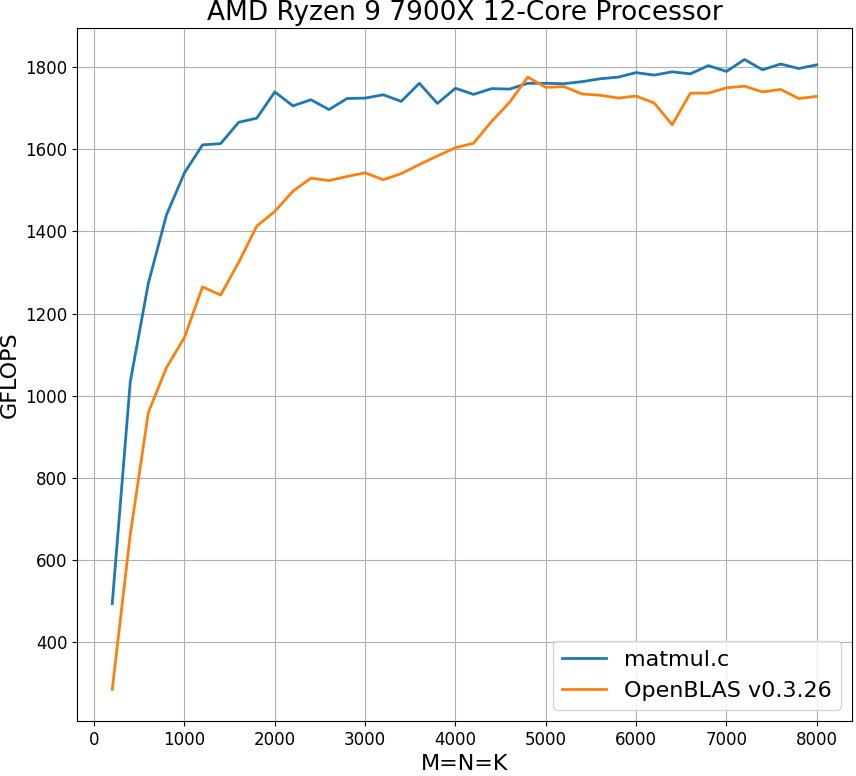
TL;DR The code is available at matmul.c. In this tutorial we’ll step-by-step optimize multi-threaded fp32 matrix multiplication on CPU outperforming OpenBLAS on wide range of matrix sizes. The algorithm follows the BLIS design and is implemented in simple, scalable C code parallelized with OpenMP. Although the code targets a wide variety of x86 processors with FMA3 and AVX2 instructions, please don’t expect peak performance without fine-tuning hyperparameters, such as the number of threads, kernel, and block sizes, unless you’re running it on a Zen3/4/5 CPU. Additionally, on AVX-512 CPUs, the OpenBLAS implementation might be notably faster due to AVX-512 instructions, which were intentionally omitted here to support a broader range of processors. The achieved performance on Ryzen 7900X and Ryzen 7700 is shown below.
P.S. Interested in working together? Please refer to the homepage for my contact information.
Introduction
Matrix multiplication is an essential part of nearly all modern neural networks. Despite using matmul daily in PyTorch, NumPy, or JAX, I’ve never really thought about how it is designed and implemented internally to maximize hardware utilization. NumPy, for instance, relies on external BLAS (Basic Linear Algebra Subprograms) libraries. These libraries implement highly optimized common linear algebra operations such as dot product, matrix multiplication, vector addition, and scalar multiplication. Examples of BLAS libraries include:
- Intel MKL - optimized for Intel CPUs
- Accelerate - optimized for Apple CPUs
- BLIS - open-source, multi-vendor support
- GotoBLAS - open-source, multi-vendor support
- OpenBLAS - open-source, based on GotoBLAS
A closer look at the OpenBLAS code reveals a mix of C and low-level assembly. In fact, OpenBLAS, GotoBLAS, and BLIS are written in C/FORTRAN/Assembly and contain matmul implementations handcrafted for different CPU types. My goal was to implement matmul algorithm in pure C without assembly that would work for arbitrary matrix sizes and would be competitive with OpenBLAS at least on my CPU. At the sime time I wanted to keep the code clean and easy to understand. After some research, I found a few exciting and educational step-by-step tutorials on implementing high-performance matrix multiplication from scratch, covering both theoretical and practical aspects:
- Fast Multidimensional Matrix Multiplication on CPU from Scratch by Simon Boehm.
- Matrix Multiplication by Sergey Slotin.
- Geohot’s famous stream Can you multiply a matrix?
I highly recommend checking out these well-written and well-spoken tutorials with alternative implementations. They helped me better understand the topic and, in some sense, motivated me to write my own implementation. The reason is that all three solutions above work only for specific matrix sizes and do not really achieve OpenBLAS’ performance. They are brilliant for educational purposes but not usable as drop-in replacement for existing BLAS libraries. So, I wasn’t satisfied with the results and continued researching until I stumbled across two fascinating papers: “Anatomy of High-Performance Matrix Multiplication” and “Anatomy of High-Performance Many-Threaded Matrix Multiplication”. The former presents BLAS implementation known as GotoBLAS, developed by Kazushige Goto. The latter briefly reviews the matmul design used in BLIS library (an extended version of GotoBLAS) and discusses different parallelization strategies. I had a feeling that the BLIS matmul design could be implemented in pure C relatively straightforward and might potentially outperform OpenBLAS if implemented correctly. In the next chapters we will therefore focus on the matmul algorithm used in BLIS and re-implement it from scratch. Before we dive into the optimization process, let’s discuss how to install OpenBLAS and properly benchmark the code on CPU.
How to install and benchmark OpenBLAS
To ensure the reproducibility of your results, always specify your hardware and software environment:
- CPU: AMD Ryzen 7 7700
- CPU locked clock frequency: 4.5GHz
- RAM: 32GB DDR5 6000 MHz CL36
- OpenBLAS 0.3.26
- Compiler: GCC 11.4.0
- OS: Ubuntu 22.04.4 LTS
Important! To obtain reproducible and accurate results, minimize the number of active tasks, particularly when benchmarking multi-threaded code. It’s important to note that Windows systems generally deliver lower performance compared to Linux due to higher number of active background tasks. To guarantee consistent results, lock the CPU clock and disable auto-boost. On Ubuntu the clock speed can be locked by executing
sudo cpupower frequency-set -u CLK
sudo cpupower frequency-set -d CLK
Ensure that clock frequency is stable and doesn’t vary during the benchmark. You can monitor the CPU clock speed, for example, via
watch -n 1 grep \"cpu MHz\" /proc/cpuinfo
To multiply two float32 matrices - A of shape \(M \times K\) and B of shape \(K \times N\), for each element of the resulting matrix C of shape \(M \times N\), we need to calculate the dot product between a row of A and a column of B. This results in \(K\) (additions) + \(K\) (multiplications) = \(2K\) FLoating Point Operations (FLOP) per element of matrix C or \(2KMN\) FLOP in total. We will measure performance in terms of FLOP per second FLOP/s=FLOPS.
To benchmark OpenBLAS, start by installing it according to the installation guide. During the installation, ensure you set an appropriate TARGET and disable AVX512 instructions. For instance, if you’re using Zen4/5 CPUs, compile OpenBLAS with:
make TARGET=ZEN
Otherwise, OpenBLAS defaults to AVX512 instructions available on Zen4/5 CPUs. Once installed, FP32 matrix multiplication can be executed using:
#include <cblas.h>
cblas_sgemm(CblasColMajor, CblasNoTrans, CblasNoTrans, m, n, k, 1, A, m, B, k, 0, C, m);
Check benchmark.c for further implementation details.
Theoretical Limit
Recall the computer’s memory hierarchy (for now, ignore the layers between registers and main memory(=RAM); we will discuss them later).
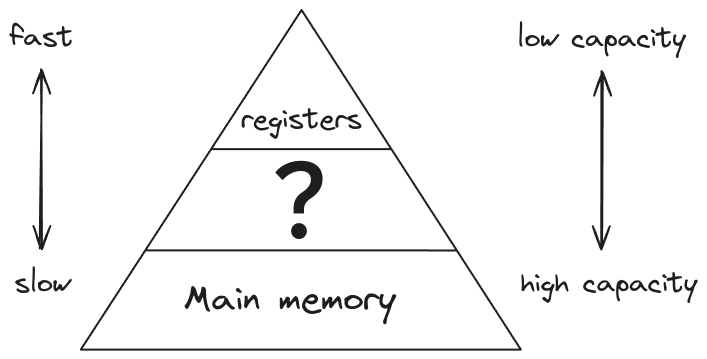
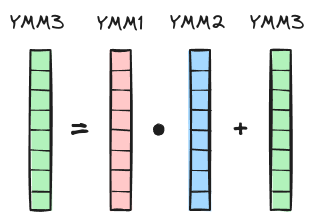
To perform arithmetic operations on data stored in RAM (off-chip memory, slow and large), the data must first be transferred to CPU and eventually stored in CPU registers (on-chip memory, fast and small). Modern x86 CPUs support SIMD (Single Instruction Multiple Data) extensions, which allow multiple pieces of data to be processed in parallel. There are various SIMD extensions, but the ones relevant to our discussion are Advanced Vector Extensions (AVX) and Fused Multiply-Add (FMA). Both AVX and FMA operate on data stored in special 256-bit YMM registers. Each YMM register can hold up to 256/32 = 8 packed single-precision (32-bit) floats. The FMA extension allows a multiply-add operation to be performed in one step on data stored in YMM registers. The corresponding assembly instruction is called VFMADD213PS (PS stands for PackedSingle) and takes three registers (YMM1, YMM2, YMM3) as input to calculate YMM1 * YMM2 + YMM3 and store the result in YMM3, hence the “213” (there are also vfmadd132ps, vfmadd231ps variants).
According to the intel intrinsics guide or https://uops.info/table.html, the throughput (TP) of fused-multiply-add is 0.5 cycles/instruction or 2 instructions/cycle:
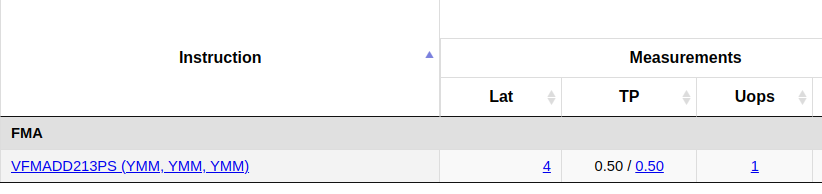
Theoretically, the CPU can execute 32 FLOP per cycle = 8 (floats in YMM register) * 2 (add + mul) * 2 (1/TP). On my machine, the CPU boosts up to stable 5.1 GHz in single-threaded tasks and up to stable 4.5 GHz in multi-threaded tasks. Therefore, a rough estimation of the maximum achievable FLOPS can be calculated as 5.1GHz * 32 FLOP/cycle = 163 GFLOPS for single-threaded matmul and 4.5GHz * 32 FLOP/cycle * 8 cores = 1152 GFLOPS for multi-threaded matmul. Starting from \(M=N=K=2000\), OpenBLAS reaches on average 92% of the theoretical maximum multi-threaded performance. Is it possible to rival OpenBLAS using plain C code, without relying on thousands of lines of low-level assembly?
Naive Implementation
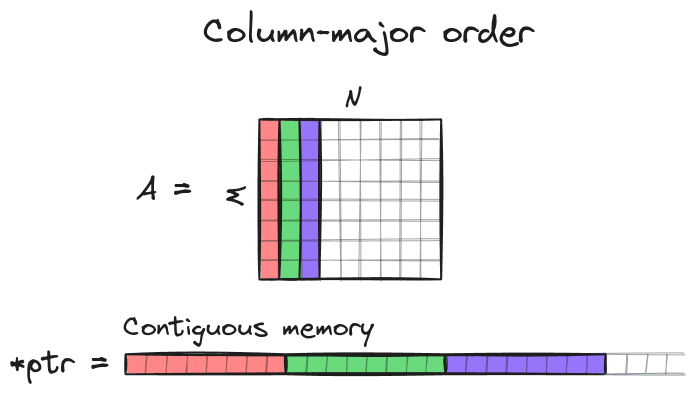
In this implementation we will assume that matrices are stored in column-major order. Matrix A of shape MxN is stored as contiguous array of length M*N and an element A[row][col] is accessed via C raw pointer ptr[col*M + row], where 0 <= col <= N-1 and 0 <= row <= M-1.
The naive algorithm

can be implemented as follows:
void matmul_naive(float* A, float* B, float* C, const int M, const int N, const int K) {
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
for (int p = 0; p < K; p++) {
C[j * M + i] += A[p * M + i] * B[j * K + p];
}
}
}
}
We iterate over all rows (first loop) and all columns (second loop) of C and for each element of C we calculate the dot product (third loop) between the corresponding rows and columns of matrices A and B. It’s always good to start with simple and robust algorithm that can later be used to test optimized implementations.
Kernel
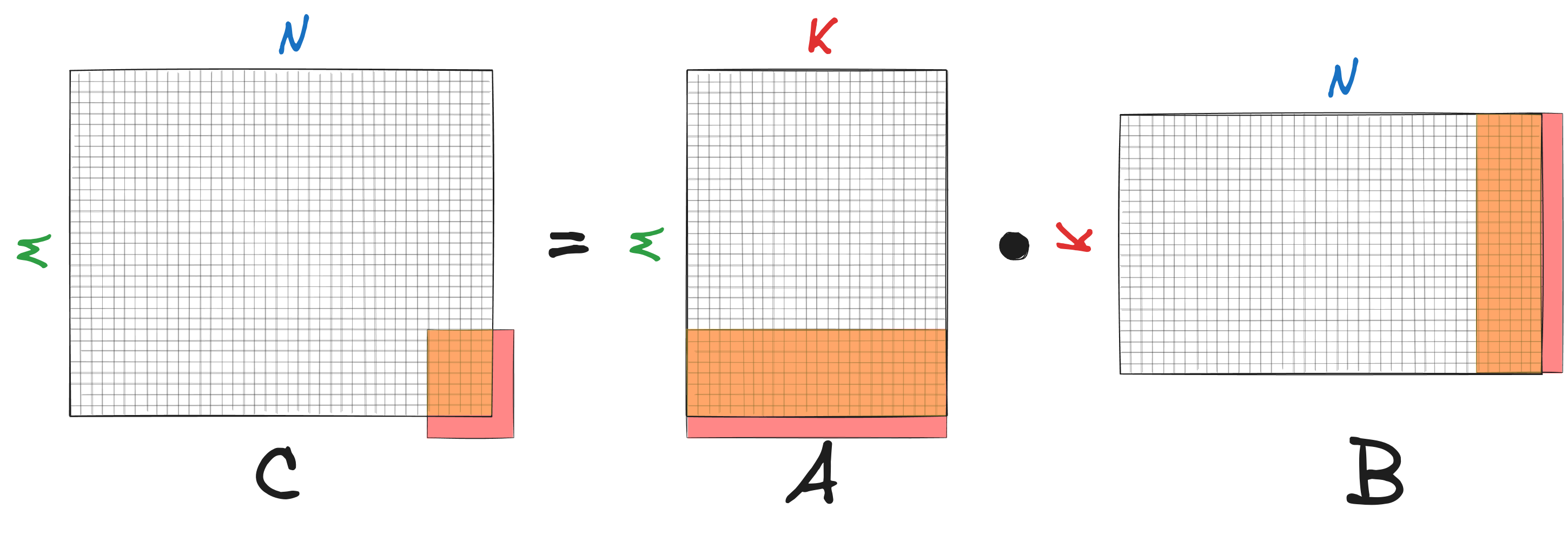
Matrix multiplication $C=AB$ can be decomposed into smaller sub-problems. The idea now is that if the smaller sub-problems can be solved fast, then the entire matmul will be fast. We first partition the matrix $C$ of shape $M \times N$ into small sub-matrices of shape $m_R \times n_R$, where $n_R \ll N$ and $m_R \ll M$. To calculate $C=AB$, we iterate over $C$ and compute each of its $m_R \times n_R$ sub-matrices.
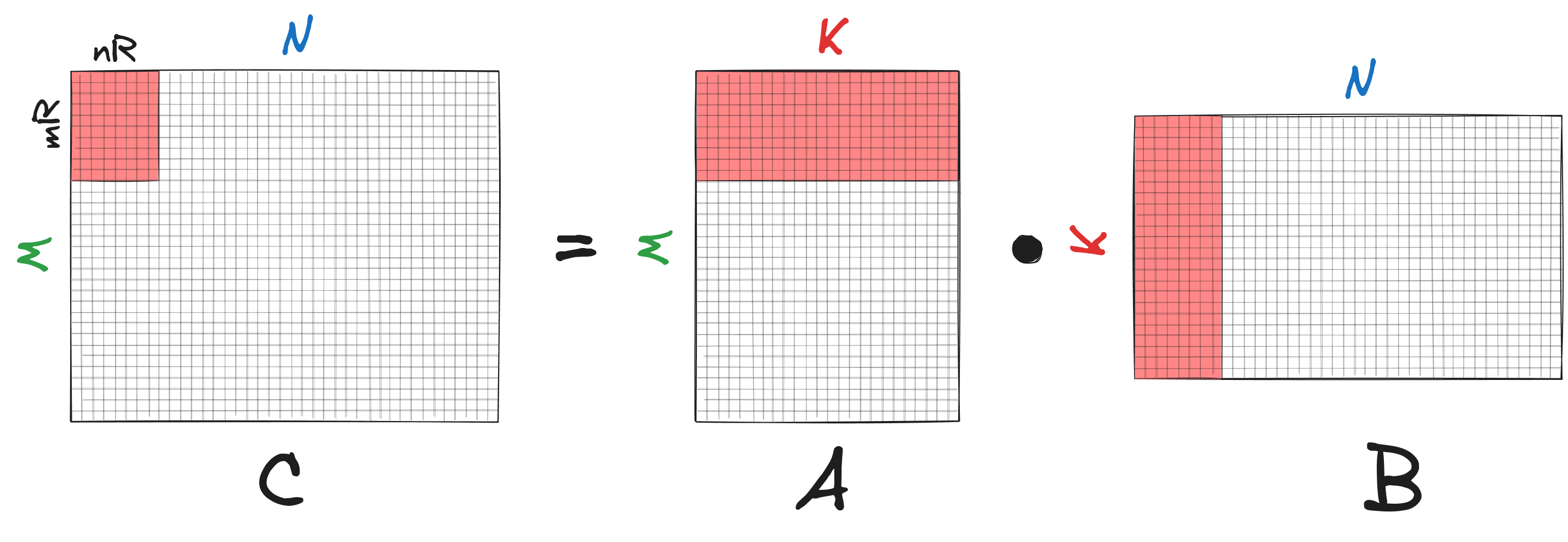
The function that calculates these tiny $m_R \times n_R$ sub-matrices $\bar{C}$ of $C$ is called kernel or micro-kernel. This is the heart of high-performance matrix multiplication. When we say that a matmul algorithm is optimized for particular CPU architecture, it often involves kernel optimization. For example, in the BLIS library, the kernels optimized for different processor types can be found under kernels.
Let’s take a closer look at the kernel.
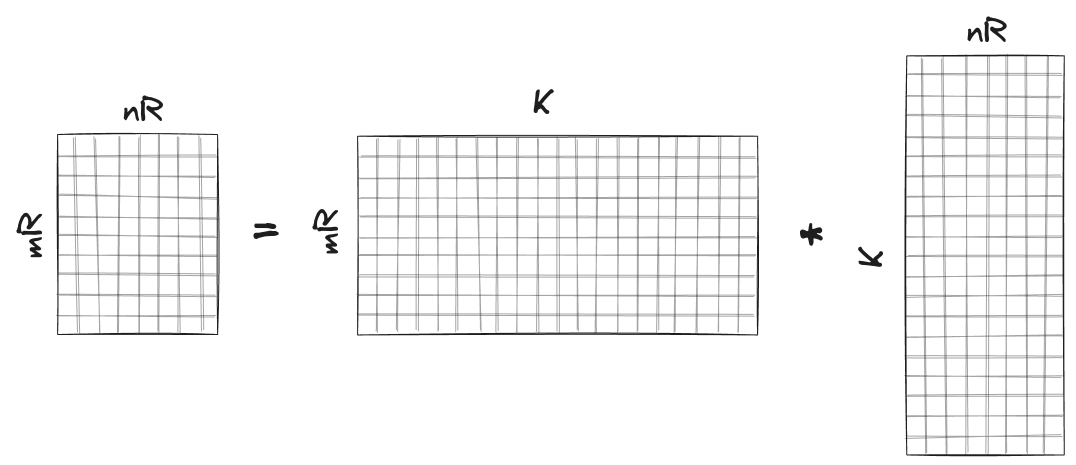
To calculate $m_R \times n_R$ sub-matrix $\bar{C}$ of matrix $C$, we multiply matrix $\bar{A}$ of size $m_R \times K$ with matrix $\bar{B}$ of size $K \times n_R$. If we would do this in naive manner using dot products, we would need to fetch $2K$ (=dot product) elements from RAM to calculate single element of $\bar{C}$ or $2K m_R n_R$ elements in total to calculate $\bar{C}$. There is, however, an alternative strategy that can reduce the number of fetched elements.
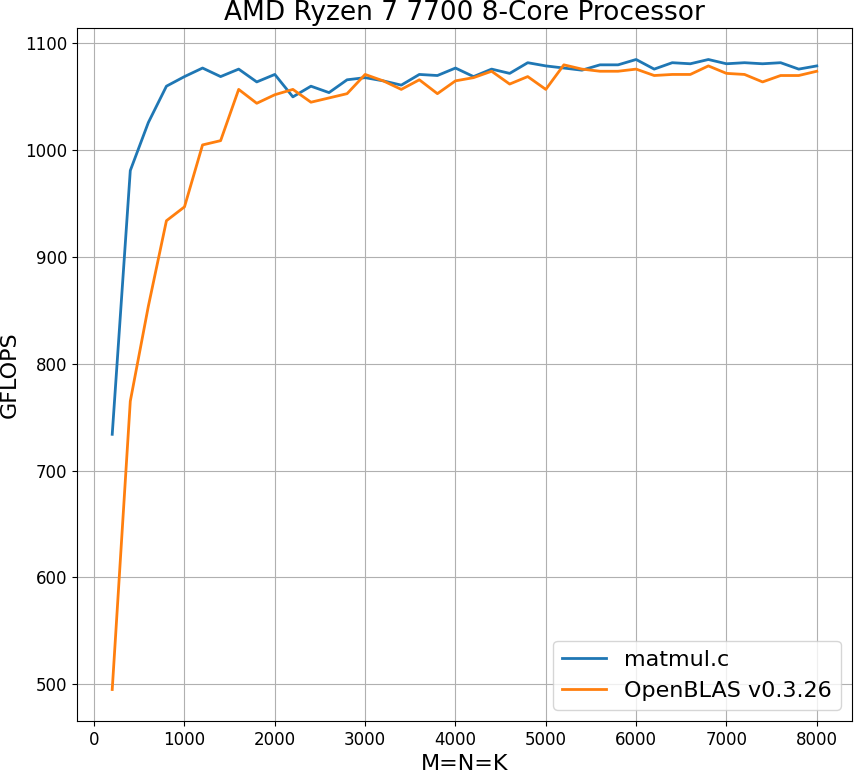
We first load matrix $\bar{C}$ into SIMD (=YMM) registers (note that we can do this because both $n_R$ and $m_R$ are small). The subscript $R$ in $n_R$ and $m_R$ stands for “registers”. Then we iterate over $K$ and in each iteration we load 1 column of $\bar{A}$ and 1 row of $\bar{B}$ into YMM registers (again, note that both the row and the column vectors are small and can be stored in the registers). Finally, we perform matrix multiplication between the column and the row vectors to update the matrix $\bar{C}$. After $K$ iterations (=rank-1 updates), the matrix $\bar{C}$ is fully computed.
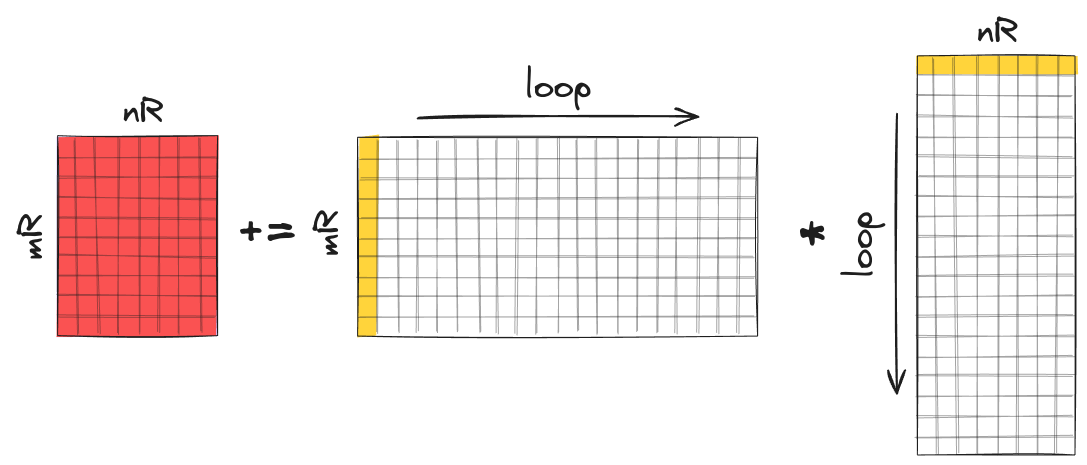
Example of matrix multiplication between a column and a row vector. Each column of the resulting matrix is computed by multiplying vector $\mathbf{u}$ with scalar element of the row vector.
Overall we fetched $(m_R + n_R)K + m_R n_R \approx (m_R + n_R)K$ elements into the registers. Compared to the naive strategy, we reduced the number by a factor of
\[\frac{2m_Rn_RK}{(m_R + n_R)K} = \frac{2m_Rn_R}{m_R + n_R}\]The factor is maximized when both $m_R$, $n_R$ are large and $m_R = n_R$. The values $m_R$ and $n_R$ are usually limited by the available memory in the registers.
Now, let’s explore how rank-1 update can be implemented using SIMD instructions. Each rank-1 update is a matrix multiplication between a column of $\bar{A}$ and a row of $\bar{B}$. Note how single column of $\bar{C}$ is updated via scalar-vector multiplication between column of $\bar{A}$ and scalar element of row of $\bar{B}$. The FMA extension allows us to efficiently compute the update and scalar-vector multiplication using a fused multiply-add instruction. To do this, we first load the matrix $\bar{C}$ and a column of $\bar{A}$ into YMM registers. Next, we broadcast the first scalar element of a row in $\bar{B}$ into a vector and load it into a YMM register. The FMA instruction is then executed to update the first column of $\bar{C}$. We repeat this process for the remaining scalar elements in the row of $\bar{B}$ to update the corresponding columns of $\bar{C}$. The parameter $m_R$ determines how many elements are stored in column of $\bar{A}$ and how many YMM registers we need to load them. Since one YMM register contains 8 floats, we assume that $m_R$ is a multiple of 8 (8, 16, 24, 32…). Then the number of YMM registers required to load one column of $\bar{A}$ can be computed as $m_R / 8$. Note that we need only one YMM register to load broadcasted scalar element of $\bar{B}$, as the same YMM Register can be reused in FMA instructions for each of $m_R / 8$ registers.
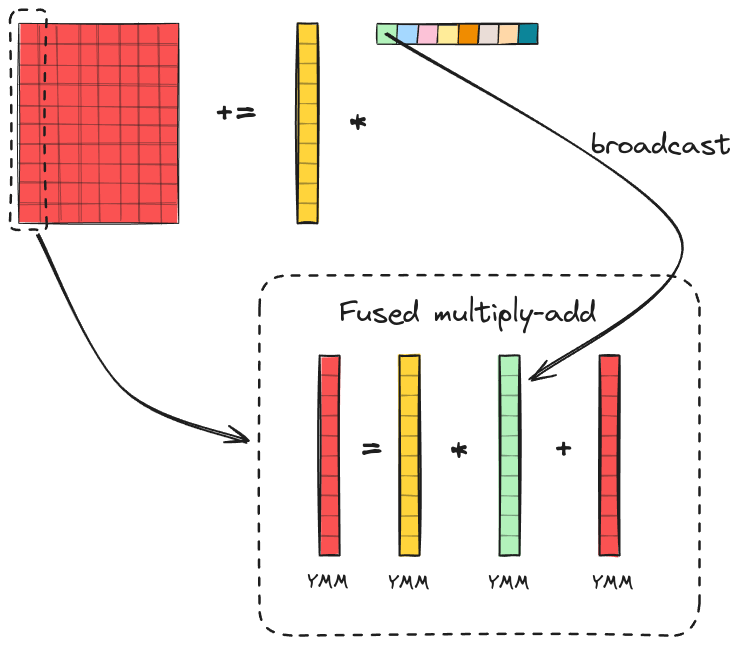
Thus, the complete algorithm for single rank-1 update of matrix $\bar{C}$ is as follows:
- Load matrix $\bar{C}$ into YMM registers
- Load column vector of matrix $\bar{A}$
- Set n = 1
- Load n-th scalar element of row vector of $\bar{B}$, broadcast it to a vector and place into single YMM register.
- Update n-th column of $\bar{C}$ via fused matrix multiply
- Increment n by 1.
- Repeat steps 4-6 until all columns of $\bar{C}$ are updated.
The last thing we need to discuss before implementing the kernel in C is how to choose the kernel size = $m_R$ and $n_R$. CPUs that support AVX instructions have 16 YMM registers. From our previous observations, we know that we need $n_R m_R / 8$ registers to store the matrix $\bar{C}$, $m_R/8$ registers to store the column vector of $\bar{A}$ and 1 register for the broadcasted vector of $\bar{B}$. We want $m_R, n_R$ as large as possible and satisfying the following conditions
- $n_R m_R/8 + m_R/8 + 1 <= 16$
- $m_R$ is a multiple of 8
In theory we also want $m_R \approx n_R$ to minimize the number of fetched elements. However, in practice, I’ve found out that the non-square $m_R \times n_R= 16 \times 6$ kernel shows the best results on my machine. You are free to try out different kernel sizes, for example, $8 \times 12$, $8 \times 13$, $8 \times 14$ and compare the performance on your CPU.
Let’s implement the $16 \times 6$ kernel in C. The code can be found at matmul_kernel.c. To use the SIMD instructions we need to include the immintin.h library.
#include <immintrin.h>
the kernel function is declared as follows:
void kernel_16x6(float* A, float* B, float* C, const int M, const int N, const int K);
The function takes as input 3 matrices + their dimensions and calculates a $16\times6$ sub-matrix $\bar{C}$ of $C$. Inside the function, first, declare the variables that reside in YMM registers:
__m256 C_buffer[6][2];
__m256 b_packFloat8;
__m256 a0_packFloat8;
__m256 a1_packFloat8;
The __m256 datatype is a vector of 8 floats (8x32 = 256 bits) that resides in YMM register. C_buffer is a 16x6 sub-matrix of $C$ stored in YMM registers. The second dimension of C_buffer is 2, because we need 16/8=2 registers to store 16 elements. b_packFloat8 is used to load broadcasted scalar element of row of $\bar{B}$ and a0_packFloat8, a1_packFloat8 are used to load one column vector of $\bar{A}$ that contains 16 floats (= 2 YMM registers).
Next, we load the sub-matrix $\bar{C}$ into YMM registers:
for (int j = 0; j < 6; j++) {
C_buffer[j][0] = _mm256_loadu_ps(&C[j * M]);
C_buffer[j][1] = _mm256_loadu_ps(&C[j * M + 8]);
}
SIMD C functions are well documented and can be found in the Intel Intrinsics Guide. For example, _mm256_loadu_ps
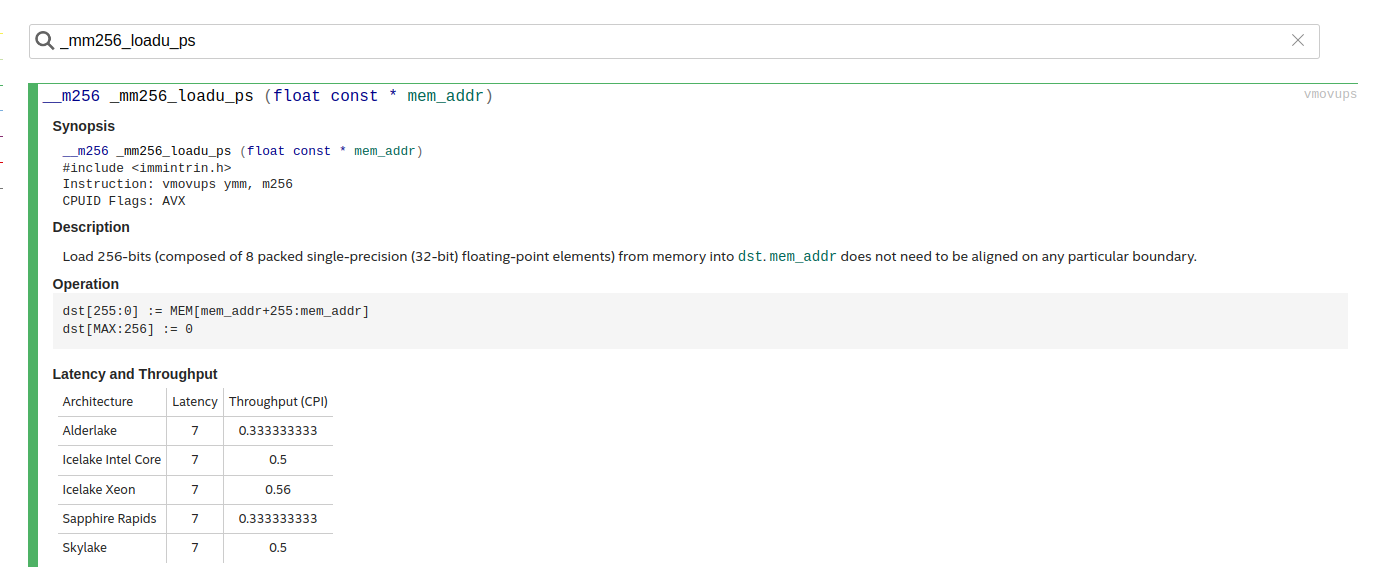
In the next step, we iterate over K and, in each iteration, load column vector of $\bar{A}$, broadcast scalar value of $\bar{B}$ to a vector, and perform a fused multiply-add operation to update single column of C_buffer:
for (int p = 0; p < K; p++) {
a0_packFloat8 = _mm256_loadu_ps(&A[p * M]);
a1_packFloat8 = _mm256_loadu_ps(&A[p * M + 8]);
b_packFloat8 = _mm256_broadcast_ss(&B[p]);
C_buffer[0][0] = _mm256_fmadd_ps(a0_packFloat8, b_packFloat8, C_buffer[0][0]);
C_buffer[0][1] = _mm256_fmadd_ps(a1_packFloat8, b_packFloat8, C_buffer[0][1]);
...
}
Then repeat the step for the remaining 5 columns. We manually unroll the loop when updating 6 columns of C_buffer so that the compiler can optimize the code.
Finally, we write the sub-matrix C_buffer back to C:
for (int j = 0; j < 6; j++) {
_mm256_storeu_ps(&C[j * M], C_buffer[j][0]);
_mm256_storeu_ps(&C[j * M + 8], C_buffer[j][1]);
}
To perform matrix multiplication, we simply iterate over the matrix $C$ and apply the kernel function:
#define MR 16
#define NR 6
void matmul_kernel(float* A, float* B, float* C, const int M, const int N, const int K) {
assert(M % MR == 0);
assert(N % NR == 0);
for (int i = 0; i < M; i += MR) {
for (int j = 0; j < N; j += NR) {
kernel_16x6(&A[i], &B[j * K], &C[j * M + i], M, N, K);
}
}
}
We can check the assembly code produced by the compiler via
gcc -O2 -mno-avx512f -march=native matmul_kernel.c -S > matmul_kernel.txt
to ensure that the SIMD instructions and the YMM registers are utilized:
vbroadcastss (%rsi,%rbp,4), %ymm14
vbroadcastss (%rbx,%rbp,4), %ymm15
vfmadd231ps %ymm14, %ymm12, %ymm3 # ymm3 = (ymm12 * ymm14) + ymm3
vfmadd231ps %ymm14, %ymm13, %ymm1 # ymm1 = (ymm13 * ymm14) + ymm1
vbroadcastss (%r13,%rbp,4), %ymm14
vfmadd231ps %ymm12, %ymm15, %ymm11 # ymm11 = (ymm15 * ymm12) + ymm11
vfmadd231ps %ymm15, %ymm13, %ymm10 # ymm10 = (ymm13 * ymm15) + ymm10
vfmadd231ps %ymm14, %ymm12, %ymm2 # ymm2 = (ymm12 * ymm14) + ymm2
vfmadd231ps %ymm14, %ymm13, %ymm0 # ymm0 = (ymm13 * ymm14) + ymm0
vbroadcastss (%r12,%rbp,4), %ymm14
vfmadd231ps %ymm14, %ymm12, %ymm5 # ymm5 = (ymm12 * ymm14) + ymm5
vfmadd231ps %ymm14, %ymm13, %ymm4 # ymm4 = (ymm13 * ymm14) + ymm4
vbroadcastss (%r15,%rbp,4), %ymm14
vfmadd231ps %ymm14, %ymm12, %ymm7 # ymm7 = (ymm12 * ymm14) + ymm7
vfmadd231ps %ymm14, %ymm13, %ymm6 # ymm6 = (ymm13 * ymm14) + ymm6
vbroadcastss (%r14,%rbp,4), %ymm14
vfmadd231ps %ymm14, %ymm12, %ymm9 # ymm9 = (ymm12 * ymm14) + ymm9
vfmadd231ps %ymm14, %ymm13, %ymm8 # ymm8 = (ymm13 * ymm14) + ymm8
Masking And Packing
You might notice that the current kernel implementation works only for matrix sizes that are multiples of $m_R$ and $n_R$. To make the algorithm work for arbitrary matrix sizes, we need to handle edge cases where the kernel doesn’t fully overlap with matrix $C$.
First of all, we when loading and storing the elements of $C$, we should pick the elements only within the matrix boundary. The case where the number of overlapped columns $n$ is less than $n_R$ is straightforward - we simply iterate over $n$ columns within the $C$ boundary:
// n - number of overlapped columns within C boundary
// "j<n" instead "j<6", since n can be less than 6.
for (int j = 0; j < n; j++) {
C_buffer[j][0] = _mm256_loadu_ps(&C[j * M]);
C_buffer[j][1] = _mm256_loadu_ps(&C[j * M + 8]);
}
Handling the case where the number of overlapped rows $m$ differs from $m_R$ is a bit trickier because _mm256_loadu_ps loads 8 elements at once. Fortunately, there is a function called _mm256_maskload_ps which loads 8 floats based on mask bits associated with each data element. It takes as input 2 arguments: const float* data and __m256i mask. __m256i is a 256-bit vector of 8x32-bit integers. The most significant bit (MSB) of each integer represents the mask bits. If a mask bit is zero, the corresponding value in the memory location is not loaded and the corresponding field in the return value is set to zero. For example, MSB of unsigned integer 2147483648 (binary representation 10000000 00000000 00000000 00000000) is 1, hence corresponding float in data will be loaded. On the other hand, MSB of unsigned integer 2147483647 (binary format 01111111 11111111 11111111 11111111) is 0, hence the corresponding float in data will not be loaded. The function _mm256_maskstore_ps works similarly, except it stores data instead of loading.
If $m \neq m_R$ , we create integer masks by left-shifting the unsigned integer 65535 (=00000000 00000000 11111111 111111111 in binary format) depending on the number of overlapped rows $m$. The function _mm256_setr_epi32 creates an 8-integer vector from 8 32-bit integers.
__m256i masks[2];
if (m != 16) {
const unsigned int bit_mask = 65535;
masks[0] = _mm256_setr_epi32(bit_mask << (m + 15), bit_mask << (m + 14),
bit_mask << (m + 13), bit_mask << (m + 12),
bit_mask << (m + 11), bit_mask << (m + 10),
bit_mask << (m + 9), bit_mask << (m + 8));
masks[1] = _mm256_setr_epi32(bit_mask << (m + 7), bit_mask << (m + 6),
bit_mask << (m + 5), bit_mask << (m + 4),
bit_mask << (m + 3), bit_mask << (m + 2),
bit_mask << (m + 1), bit_mask << m);
for (int j = 0; j < n; j++) {
C_buffer[j][0] = _mm256_maskload_ps(&C[j * M], masks[0]);
C_buffer[j][1] = _mm256_maskload_ps(&C[j * M + 8], masks[1]);
}
}
The same masks are used to store the results back after rank-1 updates.
Update 23.07.2024 Although at first glance the usage of sequential
_mm256_setr_epi32and scalar bit shifting may seem slow, the compiler is able to auto-vectorize the operations using combinations ofvpadddandvpsllvdinstructions. To be compiler-agnostic and vectorize the code manually, one can alternatively store the mask asstatic int8_tarray of size 32 and load it’s elements at offsets16-mand8-m. For example,static int8_t mask_32[32] __attribute__((aligned(64))) = {-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}; packed_masks[0] = _mm256_cvtepi8_epi32(_mm_loadu_si64(&mask_32[16 - m])); packed_masks[1] = _mm256_cvtepi8_epi32(_mm_loadu_si64(&mask_32[16 - m + 8]));
Additionally, we copy and pad with zeros (if needed) $m \times K$, $K \times n$ blocks of $A$ and $B$ into arrays with static shapes $m_R \times K$, $n_R \times K$.
void pack_blockA(float* A, float* blockA_packed, const int m, const int M,
const int K) {
for (int p = 0; p < K; p++) {
for (int i = 0; i < m; i++) {
*blockA_packed = A[p * M + i];
blockA_packed++;
}
for (int i = m; i < MR; i++) {
*blockA_packed = 0.0;
blockA_packed++;
}
}
}
These blocks with static shapes are then passed into the kernel, so that the FMA instructions inside the kernel remain unchanged and can be optimized during the compilation. The code is available at matmul_pack_mask.c
void matmul_pack_mask(float* A, float* B, float* C, float* blockA_packed,
float* blockB_packed, const int M, const int N,
const int K) {
for (int i = 0; i < M; i += MR) {
const int m = min(MR, M - i);
pack_blockA(&A[i], blockA_packed, m, M, K);
for (int j = 0; j < N; j += NR) {
const int n = min(NR, N - j);
pack_blockB(&B[j * K], blockB_packed, n, N, K);
kernel_16x6(blockA_packed, blockB_packed, &C[j * M + i], m, n, M, N, K);
}
}
}
Now, let’s optimize the data reuse and cache management.
Caching
Recall the CPU’s memory system diagram. Initially, we’ve ignored the intermediate layer between main-memory (DRAM) and the CPU’s registers - the CPU Cache.
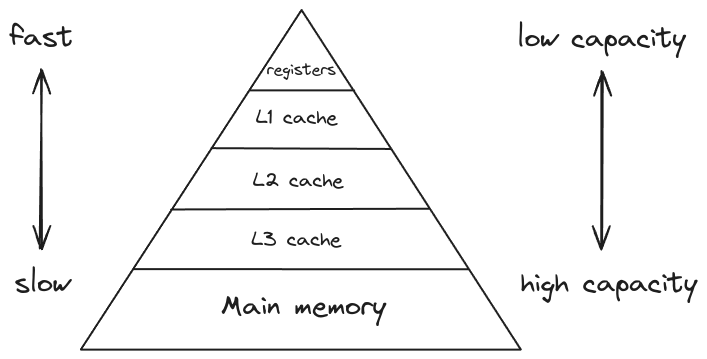
Unlike DRAM, the cache is on-chip memory used to store frequently and recently accessed data from main memory. This minimizes data transfers between main memory and registers. Although faster than DRAM, the cache has limited capacity. CPUs typically employ a multi-level cache hierarchy for efficient data access. Levels like L1, L2, and L3 offer progressively larger capacities but slower access times, with L1 being the fastest and closest to the core.
 Intel Core i9-13900K labelled die shot. Source: How are Microchips Made?
Intel Core i9-13900K labelled die shot. Source: How are Microchips Made?
To enhance access speed, CPUs transfer data between main memory and cache in fixed-size chunks called cache lines or cache blocks. When a cache line is transferred, a corresponding cache entry is created to store it. On Ryzen 7700, the cache line size is 64 bytes. The cache takes advantage of how we typically access data. When a single floating-point number from a continuous array in memory is requested, the cache cleverly grabs the next 15 floats along the way and stores them as well. This is why reading data sequentially from a contiguous array is much faster than jumping around to random memory locations. When the processor needs to read or write to a memory location, it first checks the cache for a corresponding entry. If the processor finds the memory location in the cache, a cache hit occurs. However, if the memory location is not found in the cache, a cache miss occurs. In the case of a cache miss, the cache allocates a new entry and copies the data from main memory. If the cache is full, a cache replacement policy kicks in to determine which data gets evicted to make room for new information. Several cache replacement policies exist, with LRU (Least Recently Used), LFU (Least Frequently Used), and LFRU (Least Frequently Recently Used) being the most widely used.
Similar to registers, once data is loaded into the cache, we want to reuse the data as much as possible to reduce main memory accesses. Given the cache’s limited capacity, storing entire input matrices $C, B, A$ in the cache isn’t feasible. Instead, we divide them into smaller blocks, load these blocks into the cache, and reuse them for rank-1 updates. This technique is often referred to as tiling or cache blocking, allowing us to handle matrices of arbitrary size effectively.
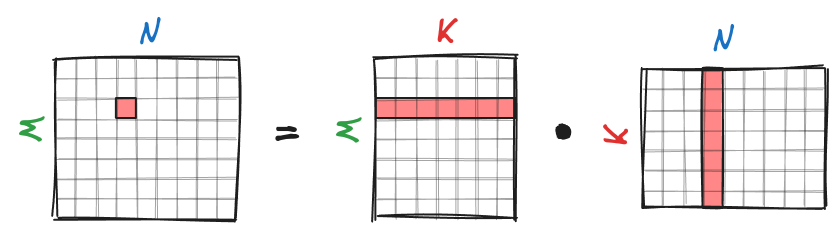
The single-threaded matrix multiplication with cache blocking can be visualized as shown in the image borrowed from the official BLIS repository:
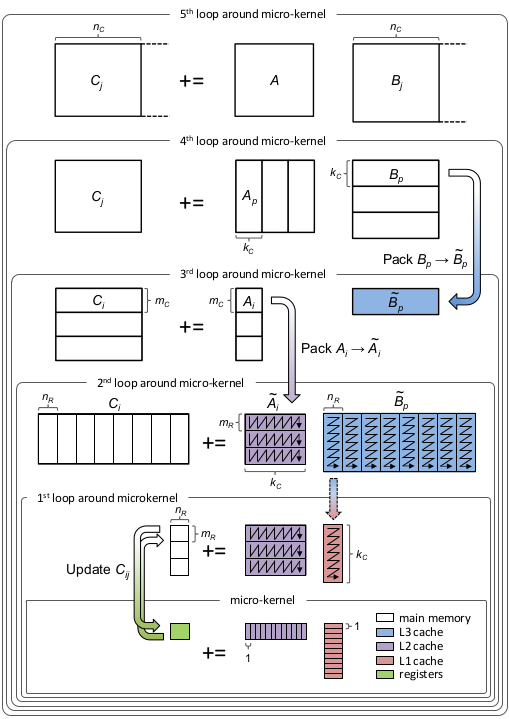
Let’s step through the diagram and discuss it. In the outer-most loop (5th loop) we iterate over dimension $N$, dividing matrix $C$ into blocks $C_j$ of size $M \times n_c$ and matrix $B$ into blocks $B_j$ of size $K \times n_c$. The subscript $c$ in $n_c$ stands for cache. In the 4th loop we iterate over dimension $K$ and divide matrix $A$ into $A_j$ of size $M \times k_c$ and $B_j$ into $B_p$ of size $k_c \times n_c$. Notice $B_p$ has fixed, limited size and can now be loaded into the cache. $B_p$ is packed into $\tilde{B}_p$, padded with zeros, if necessary, and loaded into the L3 cache. I In the 3rd loop we iterate over dimension $M$ and divide $C_j$ into $C_i$ (there is a typo in the diagram) of size $m_c \times n_c$ and $A_p$ into $A_j$ of size $m_c \times k_c$. Matrix $A_j$ is now restricted in size and can be loaded entirely into the L2 cache. $A_j$ is packed into $\tilde{A}_j$ and padded with zeros if needed. Note how we reuse the same $\tilde{B}_p$ block from the L3 cache for different $A_j$ blocks. Both $m_c$ and $n_c$ are chosen to be a multiple of $m_R$ and $n_R$ respectively.
In the last two loops we simply iterate over cached blocks and divide them into $m_R \times k_c$ and $k_c \times n_R$ panels. These panels are then passed to the kernel to perform rank-1 updates on the $m_R \times n_R$ sub-matrix of $C$, similarly to what we have already done in the previous chapter. Each panel of $\tilde{B}_p$ is loaded into the L1 cache and reused for multiple panels of $\tilde{A}_j$. Keep in mind that $\tilde{A}_j$ and $\tilde{B}_p$ are packed differently. During rank-1 updates we sequentially read a panel of $\tilde{A}_j$ column by column and a panel of $\tilde{B}_p$ row by row. Thus, each panel inside $\tilde{A}_j$ is stored in column-major order, while each panel inside $\tilde{B}_p$ is stored in row-major order.
Different CPU models have different cache sizes. To achieve peak performance, it’s crucial to optimize three key parameters: cache sizes for L1, L2, and L3 cashes (represented by $k_c$, $m_c$, and $n_c$ respectively). Theoretically, these parameters should be chosen so that:
- $k_c \times n_c$ fills the entire L3 cache.
- $m_c \times k_c$ fills the entire L2 cache.
- $k_c \times n_R$ fills the entire L1 cache.
While these values provide a good starting point, using larger values often leads to better performance in practice. Unfortunately (or fortunately), we cannot manually place data into the cache or control which cache levels store the data; the CPU manages this automatically using cache replacement policies. Therefore, cache blocking and cache reuse must be implemented at the algorithm level through, for example, well-designed loops and strategic data access patterns.
The implementation matmul_cache.c straightforwardly follows the algorithm depicted in the diagram:
void matmul_cache(float* A, float* B, float* C, const int M, const int N, const int K) {
for (int j = 0; j < N; j += NC) {
const int nc = min(NC, N - j);
for (int p = 0; p < K; p += KC) {
const int kc = min(KC, K - p);
pack_blockB(&B[j * K + p], blockB_packed, nc, kc, K);
for (int i = 0; i < M; i += MC) {
const int mc = min(MC, M - i);
pack_blockA(&A[p * M + i], blockA_packed, mc, kc, M);
for (int jr = 0; jr < nc; jr += NR) {
for (int ir = 0; ir < mc; ir += MR) {
const int mr = min(MR, mc - ir);
const int nr = min(NR, nc - jr);
kernel_16x6(&blockA_packed[ir * kc], &blockB_packed[jr * kc], &C[(j + jr) * M + (i + ir)], mr, nr, kc, M);
}
}
}
}
}
}
Kernel Micro-Optimizations
Instead of using arrays of __m256 to define the accumulator $\bar{C}$ and the masks
__m256 C_buffer[6][2];
__m256i masks[2];
we explicitly unroll them
__m256 C00 = _mm256_setzero_ps();
__m256 C10 = _mm256_setzero_ps();
__m256 C01 = _mm256_setzero_ps();
__m256 C11 = _mm256_setzero_ps();
__m256 C02 = _mm256_setzero_ps();
__m256 C12 = _mm256_setzero_ps();
__m256 C03 = _mm256_setzero_ps();
__m256 C13 = _mm256_setzero_ps();
__m256 C04 = _mm256_setzero_ps();
__m256 C14 = _mm256_setzero_ps();
__m256 C05 = _mm256_setzero_ps();
__m256 C15 = _mm256_setzero_ps();
__m256i packed_mask0;
__m256i packed_mask1;
By doing this, GCC can better optimize the code avoiding register spilling. Additionally, we use vector instructions to calculate the masks as follows:
static int8_t mask[32]
__attribute__((aligned(64))) = {-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0};
packed_mask0 = _mm256_cvtepi8_epi32(_mm_loadu_si64(&mask[16 - mr]));
packed_mask1 = _mm256_cvtepi8_epi32(_mm_loadu_si64(&mask[16 - mr + 8]));
The corresponding implementation can be found at matmul_optimized_kernel.c
Multithreading
There are indeed many loops that can be potentially parallelized. To achieve high-performance, we want to parallelize both packing and arithmetic operations. Let’s start with the arithmetic operations. The 5th, 4th, 3rd loops around the micro-kernel iterate over matrix dimensions in chunks of cache block sizes $n_c$, $k_c$, $m_c$. To efficiently parallelize the loops and keep all threads busy, we want number of iterations (=matrix dimension / cache block size) to be at least = number of threads (generally, the more the better). In other words, the input matrix dimension should be at least = number of threads * cache block size. As we discussed earlier, we also want cache blocks to fully occupy the corresponding cache levels. On modern CPUs, the second requirement results in cache block sizes of thousand(s) of elements. For example, on my Ryzen 7700, cache block sizes of $n_c=1535$, $m_c=1024$ attain the best performance in the single-threaded scenario. Given the number of available cores on Ryzen 7700, we need input matrices with dimensions of at least $\max(m_c, n_c) \times \text{number of cores} = 1535 \times 8 = 12280$ to be able to distribute the work over all cores.

In contrast, the last two loops iterate over cache blocks, dividing them into $m_R, n_R$ blocks. Since $n_R, m_R$ are typically very small (<20), these loops are ideal candidates for parallelization. Moreover, we can choose $m_c, n_c$ to be multiples of number of cores so that the work is evenly distributed across all cores.
On my machine, parallelizing the second and first loops jointly using collapse(2) results in the best performance:
#pragma omp parallel for collapse(2) num_threads(NTHREADS)
for (int jr = 0; jr < nc; jr += NR)
More on OpenMP here, here and here.
In the current implementation, only 1 out of 5 loops is parallelized (the 2nd loop around the micro-kernel). For many-core processors (more than 16 cores), consider utilizing nested parallelism and parallelizing 2-3 loops to increase the performance (e.g., the 5th, 3rd, and 2nd loops around the micro-kernel).
Together with arithmetic operations, we will also parallelize the packing of both $\tilde{A}$ and $\tilde{B}$:
void pack_blockA(float* A, float* blockA_packed, const int mc, const int kc, const int M)
#pragma omp parallel for num_threads(NTHREADS)
for (int i = 0; i < mc; i += MR)
void pack_blockB(float* B, float* blockB_packed, const int nc, const int kc, const int K)
#pragma omp parallel for num_threads(NTHREADS)
for (int j = 0; j < nc; j += NR)
Similar to the second loop (and the first loop) around the micro-kernel, the packing loops can be efficiently parallelized due to the high number of iterations and the flexibility of choosing $m_c, n_c$. For the multi-threaded implementation the values
\[m_c = m_R \times \text{number of threads} \times 2\] \[n_c = n_R \times \text{number of threads} \times 71\]provide the best performance on my machine, leading to the final optimized multi-threaded implementation.
Conclusion
I had a great time implementing and optimizing matrix multiplication on the CPU - it was a challenging but really fun project. I believe the best way to truly understand hardware and code optimization techniques is by getting hands-on and building something yourself. In our implementation, we used techniques like kernel optimization, cache/register blocking, and multi-threading. That said, there’s still room to make it even better, like manually managing threads with pthread and data prefetching.